How To Determine Odds In Betting

When it comes to gambling, you won’t be able to find two more essential concepts than odds and probability. They are what makes the entire thing work. Odds are used to calculate both the payout a gambler can expect to receive from a winning wager and the implied odds of an outcome happening. Probability is just the likelihood that a given result will occur.

One essential concept to remember is that while probability and odds are both related and may seem very similar, they aren’t exactly the same thing. Probability represents the likelihood that something will happen.

How to Calculate Parlay Bet Odds. A parlay bet is a single wager that requires two or more outcomes to all win. The parlay calculator allows you to input your stake & odds in American formats to. Betting School How are odds set in sports betting. Ever wondered how do bookies make odds or how do bookmakers set odds to be more accurate. If you are a punter who cares for his money then you should have, even if you don’t have the ambition to become a future trader.

It is calculated by dividing the number of wanted results by the total number of possible outcomes. Odds, on the other hand, present a ratio of wanted results to unwanted outcomes.

There are three primary ways of expressing odds. They are decimal, fractional, and moneyline (or American). No matter what odds format you use, these three types of odds all represent the same thing.

In fact, it is easy to convert one format to another, as you will see further down this guide.

Beyond governing how the entire world of sports betting works, odds play a vital role in helping a sports bettor decide if a bet is worth placing or not. All odds carry with them an implied probability, which we then compare to the real probability to determine whether a wager possesses positive value or not. A rule to live by in the gambling world is only to place bets with positive value.

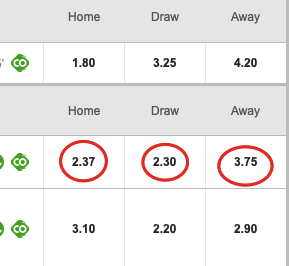
Let’s say we are gambling on the outcome of a single coin flip. Because there are only two sides of a coin, we know that each result has a 50% probability of occurring. For the sake of this example, we are betting tails. We can calculate this like so:

Our desired outcome is for the coin to land on tails, so there is one desired outcome.

We divide the amount of desired outcomes by the total amount of outcomes possible, then multiply the result by one hundred to get the probability. The formula looks like this:

1/2 = 0.5 X 100 = 50%

Now that we know the probability, let’s look at the odds being offered on this bet. For some reason, the odds for heads are set at -300, while tails are +260. This would be a very odd occurrence for such a bet but bear with me. Now we must calculate the implied probability of both lines being offered and determine which bet contains the most value.

First, we will solve the implied probability for heads. I find it easiest to convert the moneyline value to decimal odds before converting to a percentage:

Now we take our decimal odds and convert them to a percentage:

This means the implied odds are a much higher percentage than the actual 50% probability that we already calculated. A bet on heads here would be a terrible decision with a negative value.

Now we will solve for tails:

In this instance, the probability of tails landing far outweighs the implied probability determined by the odds being offered. This is a high-value bet.

Calculating the real probability and comparing that number to the implied probability set by the odds is the primary strategy with which one should approach every bet.

Understanding how to calculate betting odds and find value bets is essential to your long-term success in gambling.

In this guide, we will show you how to convert any format of odds to any other, as well as how to find the implied odds from any type of odds.

Types of Odds Formats

Decimal

Decimal odds are the favorite way to express betting lines in Europe. They are the most straightforward method of communicating odds. The decimal value is the amount that will be returned per each dollar bet. What makes this system particularly helpful is that both the amount staked and the winnings are included.

So let’s say we made a $10 bet at 3.5 odds. Our total return for winning that wager would be $35. $25 is the profit, with the other $10 being the return of our stake.

Fractional

Fractional odds are most commonly found at racetracks or for futures bets when there are entire pools of participants that can possibly win. This format expresses odds in the form of fractions such as 4/1, which would be pronounced “four-to-one.” Four-to-one odds means that you will earn $4 for every $1 that you stake.

Sometimes the fractions will be less straightforward. You may see numbers like 9/2, for example. To calculate the return on a 9/2 bet, let’s pretend that we bet $20 at 9/2 odds for a horse race.

Unlike decimals, fractional odds provide the total payout. They calculate the winnings only. To determine the total amount that you will receive for a winning bet, simply solve the equation above and add $20 to the total. So the formula looks like this:

Moneyline/American

How To Determine Odds In Betting Explanation

The moneyline system of presenting odds utilizes negative and positive three-digit values to represent which bets are favored or underdogs. A positive number means that a play is considered the underdog. The quantity after the “+” is the amount that will be won for every $100 bet.

On the other end of the spectrum, favorites are displayed with a negative value such as -350. This means that you must bet $350 to win $100. Moneyline odds only calculate the amount potentially won on a bet, and not the total payout.

Calculating Odds

To learn how to calculate odds, let’s make things a bit more interesting with a switch from a coin toss to a roll of a six-sided die. The wager that we are making is that the die will land on 3. In this example, we are looking at one desired outcome. If there are six possible outcomes on a roll of the die, and only one outcome is desirable, that means there are five undesirable results.

Because we are calculating the odds, not the probability, we are expressing a ratio of desirable results to undesirable results. In this example, the ratio would look like this:

That means there’s one chance that we will win versus five that we will not. It is important to keep in mind that we are not calculating how likely we are to win, only the ratio of good results to bad.

Now we can calculate the odds against us winning, as well as the odds in favor of a win. To calculate the odds in favor, simply divide the one possible desired outcome by the total outcomes possible.

Conversely, the odds against our win can be solved the same way:

Converting Probability to Odds

You may want to calculate an odds ratio based on a particular probability. In order to solve this equation, we will need to express the probability as a fraction. Using the same six-sided die from before, the possibility of our number landing formatted as a fraction is 1/6.

Next, just subtract the numerator from the denominator:

The answer once again gives us the number of unwanted possible results. Now we just present the odds in ratio form, bringing us to 1:5 odds.

To solve for probability given an odds ratio, we merely reverse the equation. First, we put our odds ratio in fraction form:

Add the numerator and denominator together, which will give us the total number of potential results:

Last, just put the number of wanted outcomes over the total outcomes possible, and we’ve got our probability again!

Converting Odds

There are numerous odds calculators available online that are probably faster to use, but it’s still best that you understand the formulas for converting different odds types to other formats. Below are all of the equations required to transform any kind of odds to any other arrangement.

The odds always stay the same; they are just represented differently. At times, being able to convert formats can be extremely helpful, especially when switching to decimals when solving for implied probability.

Moneyline to Decimal

To convert positive moneyline odds, the equation is:

(Moneyline odds/100) + 1 = Decimal odds

To convert negative moneyline odds, the equation is:

(100/Moneyline odds) + 1 = Decimal odds

Moneyline to Fractional

To convert positive moneyline odds, the equation is:

(Moneyline odds/100) = Fractional Odds

To convert negative moneyline odds, the equation is:

How To Determine Odds In Betting Explanation

-100/Moneyline odds = Fractional Odds

Fractional to Decimal

(Numerator/Denominator) + 1 = decimal odds

Fractional to Moneyline

(Numerator/Denominator)

If the result is greater than or equal to 1:

100 X (Answer) = Moneyline odds

If the result is less than 1:

-100/(Answer) = Moneyline odds

Decimal to Fractional

Decimal odds – 1 = X

Put X over 1

Example:

• 3.5 – 1 = 2.5
• 2.5/1 = 5/2
• 3.5 decimal odds = 5/2 fractional

Decimal to Moneyline

If decimal odds are greater than 2:

100 X (decimal odds – 1) = Moneyline odds

If decimal odds are less than 2:

-100/(decimal odds -1) = Moneyline odds

Calculating Implied Probability

To make use of our calculations solving for real probability, we must also determine the implied probability. Implied probability converts odds into a percentage.

That percentage can then be compared to the actual likelihood of an event happening, which allows for intelligent decision making.

In the early coin toss example, we converted our odds from moneyline to decimal before solving for the implied probability. This is not necessary but is often the easiest way to complete the calculation.

From Decimal Odds

Finding implied probability from decimal odds is extremely easy. Let’s say the decimal odds are 2.5.

• 1/2.5 = 0.4
• 0.4 X 100 = 40% Implied Probability

From Moneyline Odds

Calculating implied probability for a -150 favored moneyline bet:

• (- (-150)/((-(-150)) + 100 =
• 150/(150 + 100) = 150/250 = 0.6
• 0.6 X 100 = 60% Implied Probability

Calculating implied probability for an +250 underdog moneyline bet:

• 100/(250 + 100)
• 100/350 = 0.2857
• 0.2857 X 100 = 28.57% Implied Probability

From Fractional Odds

Denominator/(denominator + numerator) X 100

• Calculate the implied probability of 15/2 odds.
• 2/(2 + 15) X 100 = 2/17 X 100 =
• 0.12 X 100 = 12 % Implied Probability

In Conclusion

Understanding what odds and probabilities are, and being able to calculate both, are fundamental skills that anyone aspiring to find any success in sports gambling must possess. The two concepts are closely related and always intertwined, but they are not the same thing.

Odds are represented in ratios of wanted results to unwanted results, while probability is a calculation of wanted outcomes divided by all possible results. Whatever number that calculation produces is the percentage of likelihood that the outcome we want will occur.

To judge whether a bet is worth making or not, calculate both the real probability and the implied probability given by the odds being offered. If the actual likelihood is higher than what’s being suggested by the odds, that bet possesses value and should be wagered on. However, if the implied probability is higher, the gamble has a negative value and should be avoided.

Some of these concepts may seem confusing now, but the more you focus on value and calculating odds and probabilities, the easier betting becomes. No longer will you fall for suckers bets offering negative value, nor will you merely make picks based on who you think should win.

The sooner your betting habits become all about identifying valuable odds and betting accordingly, the sooner you’ll see your bankroll start increasing. And that entire process begins with calculating betting odds, so you’ve come to the right place.

In gambling parlance, making a book is the practice of laying bets on the various possible outcomes of a single event. The term originates from the practice of recording such wagers in a hard-bound ledger (the 'book') and gives the English language the term bookmaker for the person laying the bets and thus 'making the book'.^[1][2]

Making a 'book' (and the notion of overround)[edit]

A bookmaker strives to accept bets on the outcome of an event in the right proportions in order to make a profit regardless of which outcome prevails. See Dutch book and coherence (philosophical gambling strategy). This is achieved primarily by adjusting what are determined to be the true odds of the various outcomes of an event in a downward fashion (i.e. the bookmaker will pay out using his actual odds, an amount which is less than the true odds would have paid, thus ensuring a profit).^[3]

The odds quoted for a particular event may be fixed but are more likely to fluctuate in order to take account of the size of wagers placed by the bettors in the run-up to the actual event (e.g. a horse race). This article explains the mathematics of making a book in the (simpler) case of the former event. For the second method, see Parimutuel betting.

It is important to understand the relationship between fractional and decimal odds. Fractional odds are those written a-b (a/b or a to b) mean a winning bettor will receive their money back plus a units for every b units they bet. Multiplying both a and b by the same number gives odds equivalent to a-b. Decimal odds are a single value, greater than 1, representing the amount to be paid out for each unit bet. For example, a bet of £40 at 6-4 (fractional odds) will pay out £40 + £60 = £100. The equivalent decimal odds are 2.5; £40 x 2.5 = £100. We can convert fractional to decimal odds by the formula D=​^b+a⁄_b. Hence, fractional odds of a-1 (ie. b=1) can be obtained from decimal odds by a=D-1.

It is also important to understand the relationship between odds and implied probabilities:Fractional odds of a-b (with corresponding decimal odds D) represent an implied probability of ​^b⁄_a+b=​¹⁄_D, e.g. 6-4 corresponds to ​⁴⁄₆₊₄ = ​⁴⁄₁₀ = 0.4 (40%).An implied probability of x is represented by fractional odds of (1-x)/x, e.g. 0.2 is (1-0.2)/0.2 = 0.8/0.2 = 4/1 (4-1, 4 to 1) (equivalently, ​¹⁄_x - 1 to 1), and decimal odds of D=​¹⁄_x.

Example[edit]

In considering a football match (the event) that can be either a 'home win', 'draw' or 'away win' (the outcomes) then the following odds might be encountered to represent the true chance of each of the three outcomes:

Home: Evens

Draw: 2-1

Away: 5-1

These odds can be represented as implied probabilities (or percentages by multiplying by 100) as follows:

Evens (or 1-1) corresponds to an implied probability of ​¹⁄₂ (50%)

2-1 corresponds to an implied probability of ​¹⁄₃ (33​¹⁄₃%)

5-1 corresponds to an implied probability of ​¹⁄₆ (16​²⁄₃%)

By adding the percentages together a total 'book' of 100% is achieved (representing a fair book). The bookmaker, in his wish to avail himself of a profit, will invariably reduce these odds. Consider the simplest model of reducing, which uses a proportional decreasing of odds. For the above example, the following odds are in the same proportion with regard to their implied probabilities (3:2:1):

Home: 4-6

Draw: 6-4

Away: 4-1

4-6 corresponds to an implied probability of ​³⁄₅ (60%)

6-4 corresponds to an implied probability of ​²⁄₅ (40%)

4-1 corresponds to an implied probability of ​¹⁄₅ (20%)

By adding these percentages together a 'book' of 120% is achieved.

Odds Calculator

The amount by which the actual 'book' exceeds 100% is known as the 'overround',^[4][5] 'bookmaker margin' ^[3] or the 'vigorish' or 'vig':^[3] it represents the bookmaker's expected profit.^[3] Thus, in an 'ideal' situation, if the bookmaker accepts £120 in bets at his own quoted odds in the correct proportion, he will pay out only £100 (including returned stakes) no matter what the actual outcome of the football match.Examining how he potentially achieves this:

A stake of £60.00 @ 4-6 returns £100.00 (exactly) for a home win.

A stake of £40.00 @ 6-4 returns £100.00 (exactly) for a drawn match

A stake of £20.00 @ 4-1 returns £100.00 (exactly) for an away win

Total stakes received — £120.00 and a maximum payout of £100.00 irrespective of the result. This £20.00 profit represents a 16​²⁄₃ % profit on turnover (20.00/120.00).

In reality, bookmakers use models of reducing that are more complicated than the model of the 'ideal' situation.

Bookmaker margin in English football leagues[edit]

Bookmaker margin in English football leagues decreased in recent years.^[6] The study of six large bookmakers between 2005/06 season and 2017/2018 season showed that average margin in Premier League decreased from 9% to 4%, in English Football League Championship, English Football League One, and English Football League Two from 11% to 6%, and in National League from 11% to 8%.

Overround on multiple bets[edit]

When a punter (bettor) combines more than one selection in, for example, a double, treble or accumulator then the effect of the overround in the book of each selection is compounded to the detriment of the punter in terms of the financial return compared to the true odds of all of the selections winning and thus resulting in a successful bet.

To explain the concept in the most basic of situations an example consisting of a double made up of selecting the winner from each of two tennis matches will be looked at:

In Match 1 between players A and B both players are assessed to have an equal chance of winning. The situation is the same in Match 2 between players C and D. In a fair book in each of their matches, i.e. each has a book of 100%, all players would be offered at odds of Evens (1-1). However, a bookmaker would probably offer odds of 5-6 (for example) on each of the two possible outcomes in each event (each tennis match). This results in a book for each of the tennis matches of 109.09...%, calculated by 100 × (​⁶⁄₁₁ + ​⁶⁄₁₁) i.e. 9.09% overround.

How To Interpret Betting Odds

There are four possible outcomes from combining the results from both matches: the winning pair of players could be AC, AD, BC or BD. As each of the outcomes for this example has been deliberately chosen to ensure that they are equally likely it can be deduced that the probability of each outcome occurring is ​¹⁄₄ or 0.25 and that the fractional odds against each one occurring is 3-1. A bet of 100 units (for simplicity) on any of the four combinations would produce a return of 100 × (3/1 + 1) = 400 units if successful, reflecting decimal odds of 4.0.

The decimal odds of a multiple bet is often calculated by multiplying the decimal odds of the individual bets, the idea being that if the events are independent then the implied probability should be the product of the implied probabilities of the individual bets. In the above case with fractional odds of 5-6, the decimal odds are ​¹¹⁄₆. So the decimal odds of the double bet is ​¹¹⁄₆×​¹¹⁄₆=1.833...×1.833...=3.3611..., or fractional odds of 2.3611-1. This represents an implied probability of 29.752% (1/3.3611) and multiplying by 4 (for each of the four equally likely combinations of outcomes) gives a total book of 119.01%. Thus the overround has slightly more than doubled by combining two single bets into a double.

In general, the combined overround on a double (O_D), expressed as a percentage, is calculated from the individual books B₁ and B₂, expressed as decimals, by O_D = B₁ × B₂ × 100 − 100.In the example we have O_D = 1.0909 × 1.0909 × 100 − 100 = 19.01%.

This massive increase in potential profit for the bookmaker (19% instead of 9% on an event; in this case the double) is the main reason why bookmakers pay bonuses for the successful selection of winners in multiple bets: compare offering a 25% bonus on the correct choice of four winners from four selections in a Yankee, for example, when the potential overround on a simple fourfold of races with individual books of 120% is over 107% (a book of 207%). This is why bookmakers offer bets such as Lucky 15, Lucky 31 and Lucky 63; offering double the odds for one winner and increasing percentage bonuses for two, three and more winners.

In general, for any accumulator bet from two to i selections, the combined percentage overround of books of B₁, B₂, ..., B_i given in terms of decimals, is calculated by B₁ × B₂ × ... × B_i × 100 − 100. E.g. the previously mentioned fourfold consisting of individual books of 120% (1.20) gives an overround of 1.20 × 1.20 × 1.20 × 1.20 × 100 − 100 = 107.36%.

Settling winning bets[edit]

In settling winning bets either decimal odds are used or one is added to the fractional odds: this is to include the stake in the return. The place part of each-way bets is calculated separately from the win part; the method is identical but the odds are reduced by whatever the place factor is for the particular event (see Accumulator below for detailed example). All bets are taken as 'win' bets unless 'each-way' is specifically stated. All show use of fractional odds: replace (fractional odds + 1) by decimal odds if decimal odds known. Non-runners are treated as winners with fractional odds of zero (decimal odds of 1). Fractions of pence in total winnings are invariably rounded down by bookmakers to the nearest penny below. Calculations below for multiple-bet wagers result in totals being shown for the separate categories (e.g. doubles, trebles etc.), and therefore overall returns may not be exactly the same as the amount received from using the computer software available to bookmakers to calculate total winnings.^[7][8]

Singles[edit]

Win single

E.g. £100 single at 9-2; total staked = £100

Returns = £100 × (9/2 + 1) = £100 × 5.5 = £550

Each-way single

E.g. £100 each-way single at 11-4 ( ​¹⁄₅ odds a place); total staked = £200

Returns (win) = £100 × (11/4 + 1) = £100 × 3.75 = £375

Returns (place) = £100 × (11/20 + 1) = £100 × 1.55 = £155

Total returns if selection wins = £530; if only placed = £155

Multiple bets[edit]

Each-Way multiple bets are usually settled using a default 'Win to Win, Place to Place' method, meaning that the bet consists of a win accumulator and a separate place accumulator (Note: a double or treble is an accumulator with 2 or 3 selections respectively). However, a more uncommon way of settling these type of bets is 'Each-Way all Each-Way' (known as 'Equally Divided', which must normally be requested as such on the betting slip) in which the returns from one selection in the accumulator are split to form an equal-stake each-way bet on the next selection and so on until all selections have been used.^[9][10] The first example below shows the two different approaches to settling these types of bets.

Double^[11][12]

E.g. £100 each-way double with winners at 2-1 ( ​¹⁄₅ odds a place) and 5-4 ( ​¹⁄₄ odds a place); total staked = £200

Note: 'Win to Win, Place to Place' will always provide a greater return if all selections win, whereas 'Each-Way all Each-Way' provides greater compensation if one selection is a loser as each of the other winners provide a greater amount of place money for subsequent selections.

Treble^[11][12]

E.g. £100 treble with winners at 3-1, 4-6 and 11-4; total staked = £100

Returns = £100 × (3/1 + 1) × (4/6 + 1) × (11/4 + 1) = £2500

Accumulator^[11][12]

E.g. £100 each-way fivefold accumulator with winners at Evens ( ​¹⁄₄ odds a place), 11-8 ( ​¹⁄₅ odds), 5-4 ( ​¹⁄₄ odds), 1-2 (all up to win) and 3-1 ( ​¹⁄₅ odds); total staked = £200

Note: 'All up to win' means there are insufficient participants in the event for place odds to be given (e.g. 4 or fewer runners in a horse race). The only 'place' therefore is first place, for which the win odds are given.

How To Determine Odds In Betting

Returns (win fivefold) = £100 × (1/1 + 1) × (11/8 + 1) × (5/4 + 1) × (1/2 + 1) × (3/1 + 1) = £6412.50

Returns (place fivefold) = £100 × (1/4 + 1) × (11/40 + 1) × (5/16 + 1) × (1/2 + 1) × (3/5 + 1) = £502.03

Total returns = £6914.53

Full-cover bets[edit]

Trixie

Yankee

Trixie, Yankee, Canadian, Heinz, Super Heinz and Goliath form a family of bets known as full cover bets which have all possible multiples present. Examples of winning Trixie and Yankee bets have been shown above. The other named bets are calculated in a similar way by looking at all the possible combinations of selections in their multiples. Note: A Double may be thought of as a full cover bet with only two selections.

Should a selection in one of these bets not win, then the remaining winners are treated as being a wholly successful bet on the next 'family member' down. For example, only two winners out of three in a Trixie means the bet is settled as a double; only four winners out of five in a Canadian means it is settled as a Yankee; only five winners out of eight in a Goliath means it is settled as a Canadian. The place part of each-way bets is calculated separately using reduced place odds. Thus, an each-way Super Heinz on seven horses with three winners and a further two placed horses is settled as a win Trixie and a place Canadian. Virtually all bookmakers use computer software for ease, speed and accuracy of calculation for the settling of multiples bets.

Full cover bets with singles[edit]

Patent

Patent, Lucky 15, Lucky 31, Lucky 63 and higher Lucky bets form a family of bets known as full cover bets with singles which have all possible multiples present together with single bets on all selections. An examples of a winning Patent bet has been shown above. The other named bets are calculated in a similar way by looking at all the possible combinations of selections in their multiples and singles.

Should a selection in one of these bets not win, then the remaining winners are treated as being a wholly successful bet on the next 'family member' down. For example, only two winners out of three in a Patent means the bet is settled as a double and two singles; only three winners out of four in a Lucky 15 means it is settled as a Patent; only four winners out of six in a Lucky 63 means it is settled as a Lucky 15. The place part of each-way bets is calculated separately using reduced place odds. Thus, an each-way Lucky 63 on six horses with three winners and a further two placed horses is settled as a win Patent and a place Lucky 31.

Algebraic interpretation[edit]

Returns on any bet may be considered to be calculated as 'stake unit' × 'odds multiplier'. The overall 'odds multiplier' is a combined decimal odds value and is the result of all the individual bets that make up a full cover bet, including singles if needed. E.g. if a successful £10 Yankee returned £461.35 then the overall 'odds multiplier' (OM) is 46.135.

If a, b, c, d... represent the decimal odds, i.e. (fractional odds + 1), then an OM can be calculated algebraically by multiplying the expressions (a + 1), (b + 1), (c + 1)... etc. together in the required manner and subtracting 1. If required, (decimal odds + 1) may be replaced by (fractional odds + 2).^[13][14]

Examples[edit]

3 selections with decimal odds a, b and c.Expanding (a + 1)(b + 1)(c + 1) algebraically gives abc + ab + ac + bc + a + b + c + 1. This is equivalent to the OM for a Patent (treble: abc; doubles: ab, ac and bc; singles: a, b and c) plus 1.Therefore to calculate the returns for a winning Patent it is just a case of multiplying (a + 1), (b + 1) and (c + 1) together and subtracting 1 to get the OM for the winning bet, i.e. OM = (a + 1)(b + 1)(c + 1) − 1. Now multiply by the unit stake to get the total return on the bet.^[15][16]

E.g. The winning Patent described earlier can be more quickly and simply evaluated by the following:

Total returns = £2 × [(4/6 + 2) × (2/1 + 2) × (11/4 + 2) − 1] = £99.33

Ignoring any bonuses, a 50 pence each-way Lucky 63 (total stake £63) with 4 winners [2-1, 5-2, 7-2 (all ​¹⁄₅ odds a place) and 6-4 (​¹⁄₄ odds a place)] and a further placed horse [9-2 (​¹⁄₅ odds a place)] can be relatively easily calculated as follows:

Returns (win part) = 0.50 × [(2/1 + 2) × (5/2 + 2) × (7/2 + 2) × (6/4 + 2) − 1] = £172.75

or more simply as 0.50 × (4 × 4.5 × 5.5 × 3.5 − 1)

Returns (place part) = 0.50 × [(2/5 + 2) × (5/10 + 2) × (7/10 + 2) × (6/16 + 2) × (9/10 + 2) − 1] = £11.79

or more simply as 0.50 × (2.4 × 2.5 × 2.7 × 2.375 × 2.9 − 1)

Total returns = £184.54

For the family of full cover bets that do not include singles an adjustment to the calculation is made to leave just the doubles, trebles and accumulators. Thus, a previously described winning £10 Yankee with winners at 1-3, 5-2, 6-4 and Evens has returns calculated by:

£10 × [(1/3 + 2) × (5/2 + 2) × (6/4 + 2) × (1/1 + 2) − 1 − [(1/3 + 1) + (5/2 + 1) + (6/4 + 1) + (1/1 + 1)]] = £999.16

In effect, the bet has been calculated as a Lucky 15 minus the singles. Note that the total returns value of £999.16 is a penny higher than the previously calculated value as this quicker method only involves rounding the final answer, and not rounding at each individual step.

In algebraic terms the OM for the Yankee bet is given by:

OM = (a + 1)(b + 1)(c + 1)(d + 1) − 1 − (a + b + c + d)

In the days before software became available for use by bookmakers and those settling bets in Licensed Betting Offices (LBOs) this method was virtually de rigueur for saving time and avoiding the multiple repetitious calculations necessary in settling bets of the full cover type.

Settling other types of winning bets[edit]

Up and down

Round Robin

A Round Robin with 3 winners is calculated as a Trixie plus three Up and Down bets with 2 winners in each.

A Round Robin with 2 winners is calculated as a double plus one Up and Down bet with 2 winners plus two Up and Down bets with 1 winner in each.

A Round Robin with 1 winner is calculated as two Up and Down bets with one winner in each.

Flag and Super Flag bets may be calculated in a similar manner as above using the appropriate full cover bet (if sufficient winners) together with the required number of 2 winner- and 1 winner Up and Down bets.

Note: Expert bet settlers before the introduction of bet-settling software would have invariably used an algebraic-type method together with a simple calculator to determine the return on a bet (see below).

Algebraic interpretation[edit]

If a, b, c, d... represent the decimal odds, i.e. (fractional odds + 1), then an 'odds multiplier' OM can be calculated algebraically by multiplying the expressions (a + 1), (b + 1), (c + 1)... etc. together in the required manner and adding or subtracting additional components. If required, (decimal odds + 1) may be replaced by (fractional odds + 2).^[13][14]

Examples[edit]

• OM (2 winners) = (2a − 1) + (2b − 1) = 2(a + b − 1)
• OM (1 winner) = a − 1

• OM (3 winners) = (a + 1) × (b + 1) × (c + 1) − 1 − (a + b + c) + 2 × [(a + b − 1) + (a + c − 1) + (b + c − 1)] = (a + 1)(b + 1)(c + 1) + 3(a + b + c) − 7
• OM (2 winners) = (a + 1) × (b + 1) − 1 − (a + b) + 2 × (a + b − 1) + (a − 1) + (b − 1) = (a + 1)(b + 1) + 2(a + b) − 5
  or more simply as OM = ab + 3(a + b) − 4
• OM (1 winner) = 2 × (a − 1) = 2(a − 1)

• OM (4 winners) = (a + 1) × (b + 1) × (c + 1) × (d + 1) − 1 − (a + b + c + d) + 2 × [(a + b − 1) + (a + c − 1) + (a + d − 1) + (b + c − 1) + (b + d − 1) + (c + d − 1)]
  = (a + 1)(b + 1)(c + 1)(d + 1) + 5(a + b + c + d) − 13
• OM (3 winners) = (a + 1) × (b + 1) × (c + 1) − 1 − (a + b + c) + 2 × [(a + b − 1) + (a + c − 1) + (b + c − 1)] + (a − 1) + (b − 1) + (c − 1) = (a + 1)(b + 1)(c + 1) + 4(a + b + c) − 10
• OM (2 winners) = (a + 1) × (b + 1) − 1 − (a + b) + 2 × (a + b − 1) + 2 × [(a − 1) + (b − 1)] = (a + 1)(b + 1) + 3(a + b) − 7
  or more simply as OM = ab + 4(a + b) − 6
• OM (1 winner) = 3 × (a − 1) = 3(a − 1)

See also[edit]

Notes[edit]

Explain How Betting Odds Work

1. ^Sidney 1976, p.6
2. ^Sidney 2003, p.13,36
3. ^ ^abcdCortis, Dominic (2015). Expected Values and variance in bookmaker payouts: A Theoretical Approach towards setting limits on odds. Journal of Prediction Markets. 1. 9.
4. ^Sidney 1976, p.96-104
5. ^Sidney 2003, p.126-130
6. ^Marek, Patrice (September 2018). 'Bookmakers' Efficiency in English Football Leagues'. Mathematical Methods in Economis - Conference Proceedings: 330–335.
7. ^Sidney 1976, p.138-147
8. ^Sidney 2003, p.163-177
9. ^Sidney 1976, p.155-156
10. ^Sidney 2003, p.170-171
11. ^ ^abcSidney 1976, p.153-168
12. ^ ^abcSidney 2003, p.169-177
13. ^ ^abSidney 1976, p.166
14. ^ ^abSidney 2003, p.169,176
15. ^Sidney 1976, p.161
16. ^Sidney 2003, p.176

References[edit]

• Cortis, D. (2015). 'Expected Values and variance in bookmaker payouts: A Theoretical Approach towards setting limits on odds'. Journal of Prediction Markets. 1. 9.
• Sidney, C (1976). The Art of Legging, Maxline International.
• Sidney, C (2003). The Art of Legging: The History, Theory, and Practice of Bookmaking on the English Turf, 3rd edition, Rotex Publishing 2003, 224pp. ISBN978-1-872254-06-7. Definitive, and extensively revised and updated 3rd edition on the history, theory, practice and mathematics of bookmaking, plus the mathematics of off-course betting, bets and their computation and liability control.

How To Count Odds In Betting

Further reading[edit]

• 'Finding an Edge', Ron Loftus, US-SC-North Charleston: Create Space., 2011, 144pp.
• 'How to make a book', Phil Bull, London: Morrison & Gibb Ltd., 1948, 160pp.
• 'The book on bookmaking', Ferde Rombola, California: Romford Press, 1984, 147pp. ISBN978-0-935536-37-9.
• The Art of Bookmaking, Malcolm Boyle, High Stakes Publishing 2006.
• Secrets of Successful Betting, Michael Adams, Raceform, 2002.
• The Mathematics of Games and Gambling, Edward W. Packel, Mathematical Association of America, 2006.
• The Mathematics of Gambling, Edward O. Thorp, L. Stuart, 1984.
• 'Maximin Hedges', Jean-Claude Derderian, Mathematics Magazine, volume 51, number 3. (May, 1978), pages 188–192.
• 'Carnap and de Finetti on Bets and the Probability of Singular Events: The Dutch Book Argument Reconsidered' Klaus Heilig, The British Journal for the Philosophy of Science, volume 29, number 4. (December, 1978), pages 325–346.
• 'Tests of the Efficiency of Racetrack Betting Using Bookmaker Odds', Ron Bird, Michael McCrae, Management Science, volume 33, number 12 (December, 1987), pages 152–156.
• 'Why is There a Favourite-Longshot Bias in British Racetrack Betting Markets', Leighton Vaughan Williams, David Paton. The Economic Journal, volume 107, number 440 (January, 1997), pages 150–158.
• Optimal Determination of Bookmakers' Betting Odds: Theory and Tests, by John Fingleton and Patrick Waldron, Trinity Economic Paper Series, Technical Paper No. 96/9, Trinity College, University of Dublin, 1999.
• 'Odds That Don't Add Up!', Mike Fletcher, Teaching Mathematics and its Applications, 1994, volume 13, number 4, pages 145–147.
• 'Information, Prices and Efficiency in a Fixed-Odds Betting Market', Peter F. Pope, David A. Peel, Economica, New Series, volume 56, number 223, (August, 1989), pages 323–341.
• 'A Mathematical Perspective on Gambling', Molly Maxwell, MIT Undergraduate Journal of Mathematics, volume 1, (1999), pages 123–132.
• 'Probability Guide to Gambling: The Mathematics of dice, slots, roulette, baccarat, blackjack, poker, lottery and sport bets', Catalin Barboianu, Infarom, 2006, 316pp. ISBN973-87520-3-5.

External links[edit]